NT50, EC50, IC50的计算
在药物研究中,经常涉及到 NT50、EC50、IC50 等概念。
NT50(half maximal neutralization titre)是达到一半生物效应的稀释倍数,数字高代表少量药物即可达到药效,因此该数值越高越好。NT50 常用于无法确定初始浓度的场景,例如表征血浆对某抗原的中和能力。
EC50/ED50(half maximal effect concentration/dose)是达到一半生物效应的浓度或剂量,越低越好。IC50/ID50(half maximal inhibitory concentration/dose)与之类似,也是越低越好,常用于描述药物的抑制效应,例如中和抗体对病毒入侵细胞的抑制,或小分子抑制剂对靶点的阻断。
IC50 案例
获得 NT50、EC50 或 IC50 的方法是高度相似的。以 IC50 为例,在不同给药浓度或稀释梯度下定量检测生物学效应(比如使用荧光定量),可获得类似的表格:
| concentration | OD |
|---|---|
| 1.4200000 | 512240 |
| 0.2840000 | 1618240 |
| 0.0568000 | 2849730 |
| 0.0113600 | 3283260 |
| 0.0022720 | 3188540 |
| 0.0004544 | 3969840 |
这组数据是在检测某抗体(下文称 AbX)的假病毒中和能力时产生的。第一列 concentration 代表抗体浓度,第二列 OD 代表荧光定量值。
当给药浓度高时,AbX 阻止病毒入侵细胞,病毒无法感复制自身,携带的报告基因就无法表达,因此 OD 值较低。给药浓度低时,大量报告基因被表达,OD 值很高。
我们要做的,就是拟合出一条类似这样的曲线,找到达到 50%抑制效果时,对应的横坐标浓度。
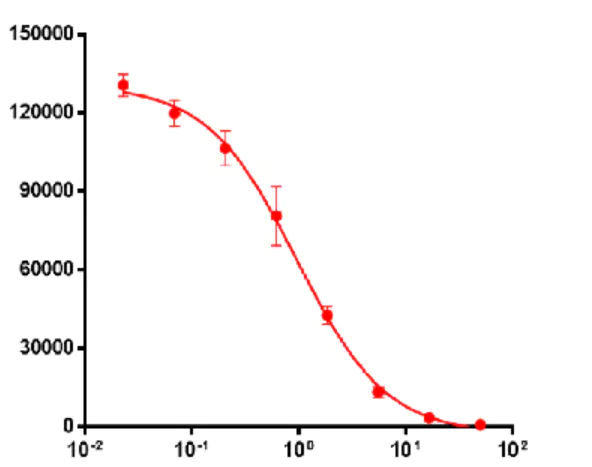
拟合这条曲线有很多种做法,显然他们的结果会有所差异。目前较常用的是四参数逻辑斯蒂回归,属于非线性回归模型,常用于生物化学的反应测定。
目标即使用下式,拟合以上浓度、反应强度数据,解出未知参数 c, d, e, b,我们就得到以上曲线了
x 为浓度、y 为反应强度,c 代表反应下限、d 代表反应上限,e 代表 IC50,b 代表 IC50 处的斜率。
有时我们通过阴性对照、阳性对照或逻辑推理,可以确定反应上下限的值。本次抗体的假病毒中和实验中,反应上限就是不加抗体的对照,数值是 3154763;反应下限就是 AbX 中和力很强、加的剂量也足够多,完全阻断病毒,荧光定量是 0。因此,c, d 这两个参数我们可以直接输入模型,拟合 e, b 即可。
实现拟合的工具也有很多,这里介绍最常用的两种:使用 R 语言、使用 Prism
使用 R 语言拟合
R 语言的 drc 包可以很方便地实现拟合、可视化,本文使用的版本是 R v4.2.3 和 drc v3.0。首先将实验结果构建为数据帧
library(drc)
x <- c(1.42, 0.284, 0.0568, 0.01136, 0.002272, 0.0004544)
y <- c(512240, 1618240, 2849730, 3283260, 3188540, 3969840)
data <- data.frame(x, y)
然后使用 drm 函数拟合。LL.4 代表四参数逻辑斯蒂模型,names 指定结果中参数显示的名称,不影响计算。fixed 允许我们输入已知参数
m <- drm(y~x, data=data,
fct=LL.4(
names=c("Slope", "Lower Limit", "Upper Limit", "IC50"),
fixed=c(NA, 0, 3154763, NA)
)
)
拟合完毕后,打印 m 即可获得 IC50 的值,或者你也可以调用 ED(m, 50) 获得(Effective Dose)。后者在需要如 IC80, IC90 等数值的时候很有用。
A 'drc' model.
Call:
drm(formula = y ~ x, data = data, fct = LL.4(names = c("Slope", "Lower Limit", "Upper Limit", "IC50"), fixed = c(NA, 0, 3154763, NA)))
Coefficients:
Slope:(Intercept) IC50:(Intercept)
1.2361 0.3166
使用 plot(m),即可获得曲线的基本图像,像这样
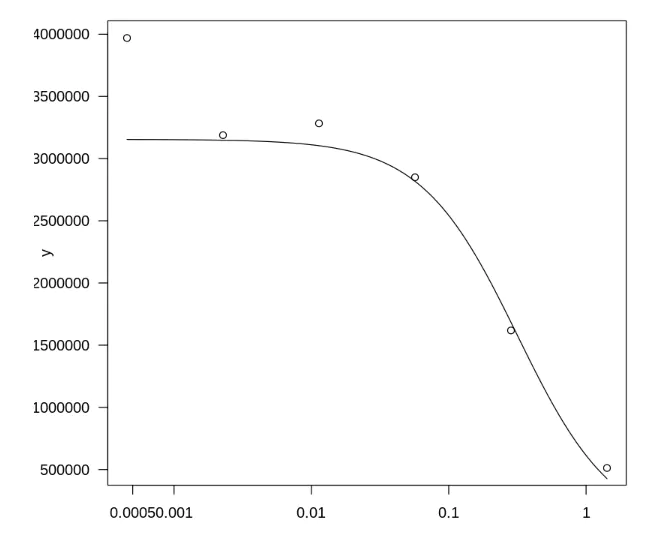
如果你更愿意通过 ggplot 绘图,以获得更高的自由度,则需要先用 predict 函数,借助模型生成一些连续的 x,y 数值对(比如 100 对),保证曲线的平滑度
x_pred <- seq(min(x), max(x), length.out = 100)
y_pred <- predict(m, newdata = data.frame(x = x_pred))
data_pred <- data.frame(x = x_pred, y = y_pred)
然后调用 ggplot 绘图
library(ggplot)
ggplot() +
geom_point(data = data, aes(x = x, y = y)) +
geom_line(data = data_pred, aes(x = x, y = y), color = "blue") +
labs(x = "Dose", y = "Response", title = "Dose-Response Curve") +
scale_x_log10() +
theme_classic()
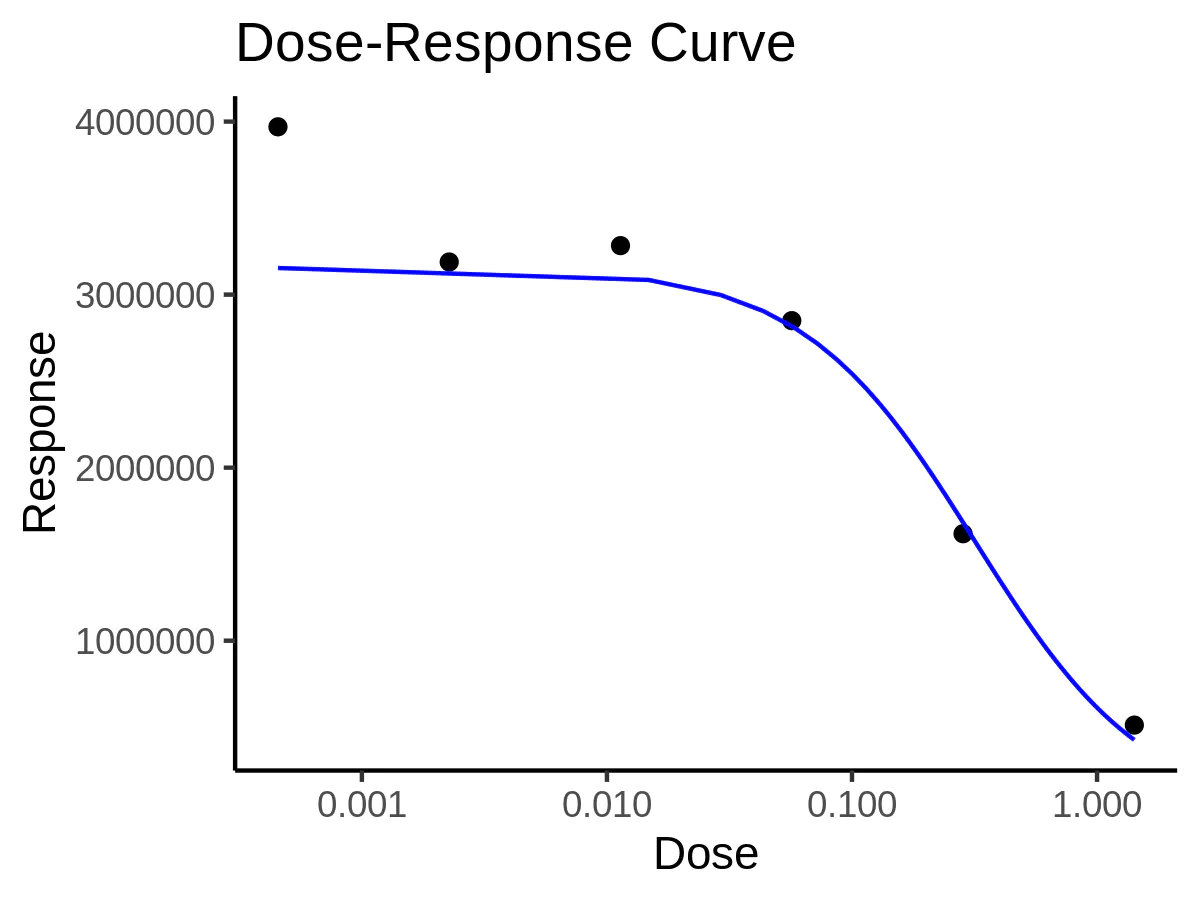
可以看到,drc 是不区分 IC50、EC50 还是 NT50 的。
使用 Prism 拟合
使用 Prism v10.2.1,在欢迎页选择 CREATE-XY,选择第一个 Y 选项,点击创建
粘贴数据到 X、Y(Group A)
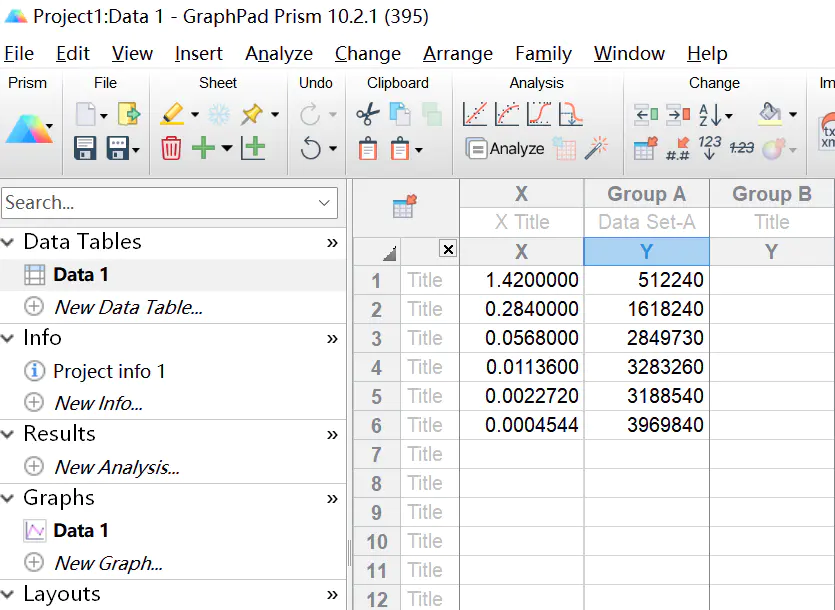
依次选择 Analyze, Regression and Curves, Nonlinear Regression (Curve Fit)
选择数据集,保持默认的 Data1 即可,确认
选择模型,在 Dose-response -Inhibition 下,找到 [Inhibitor] vs. response -- Variable slope (four parameters)。可见,Prism 严格区分了 IC50(Inhibition)、EC50(Stimulation),并且也区分 x 是原始值([Inhibitor])还是对数值(log(inhibitor))。
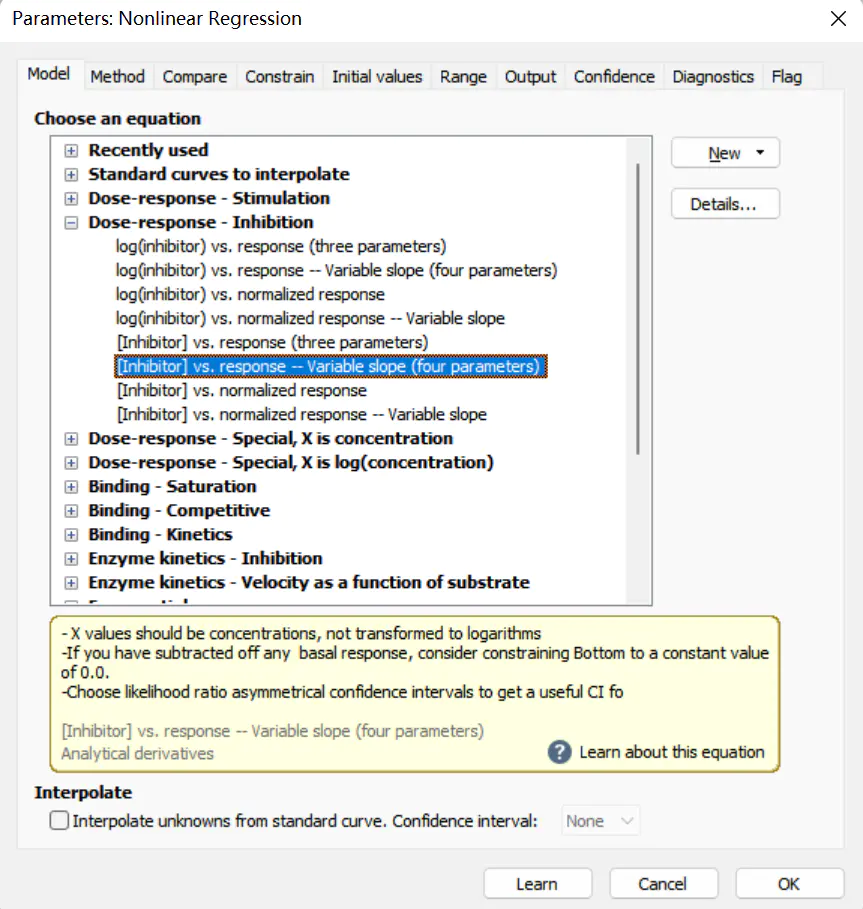
紧接着,在 Constrain 选项卡下,输入已知的 Top 和 Bottom 数值,点击确定
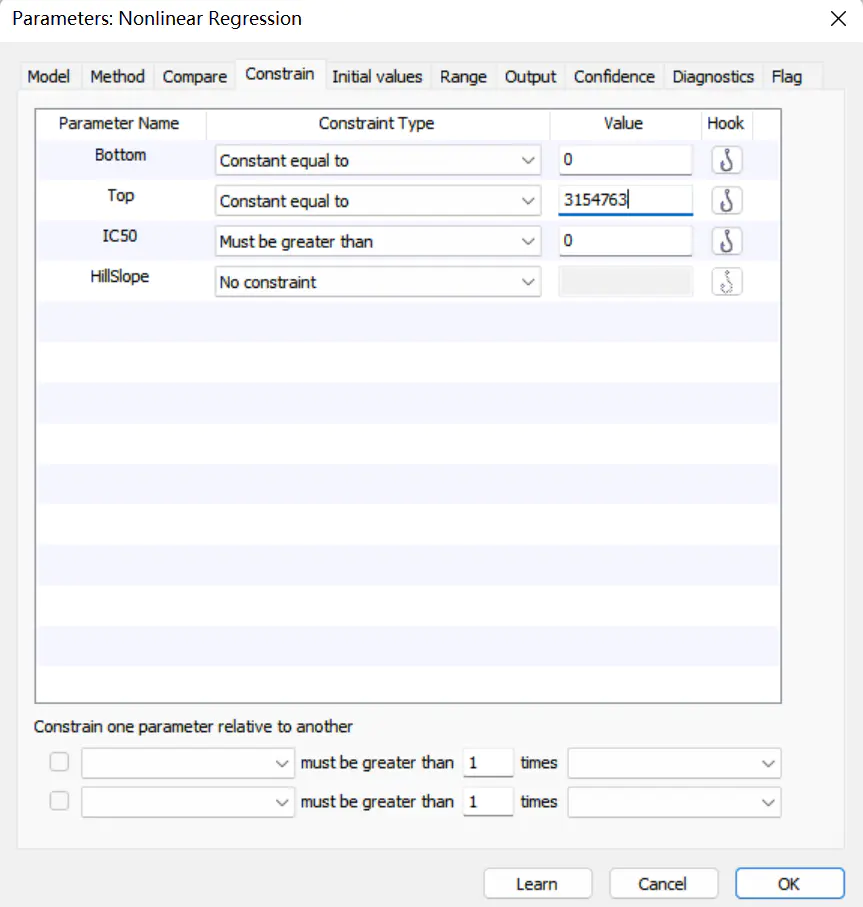
于是得到所需的各项数值。IC50 为 0.3167,与 R 语言的结果一致。另外也给出了拟合优度(Goodness of Fit),可以看到 R^2 为 0.91,说明拟合得不错。
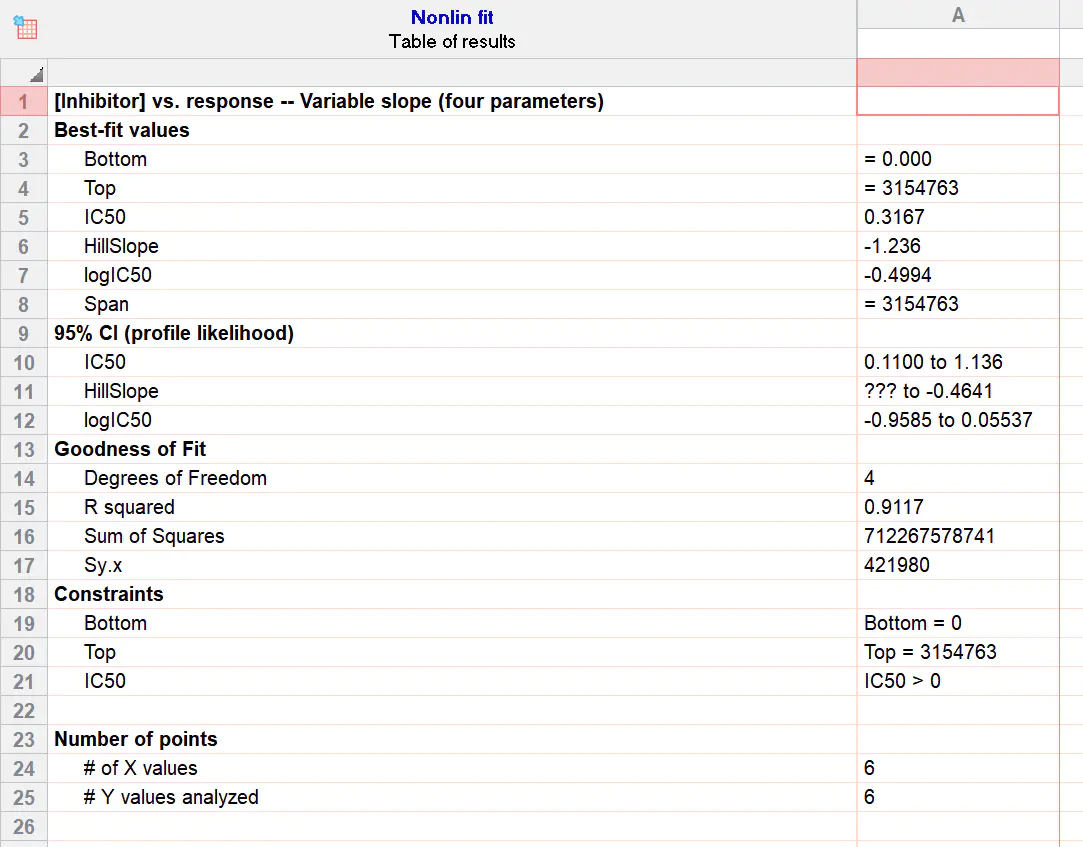
可能你也好奇选择数学形式完全相同的 Dose-response -Stimulation 会怎样。结果是拟合错误,显示 Bad initial values,EC50 随便给了个数值,且不会给出拟合优度。
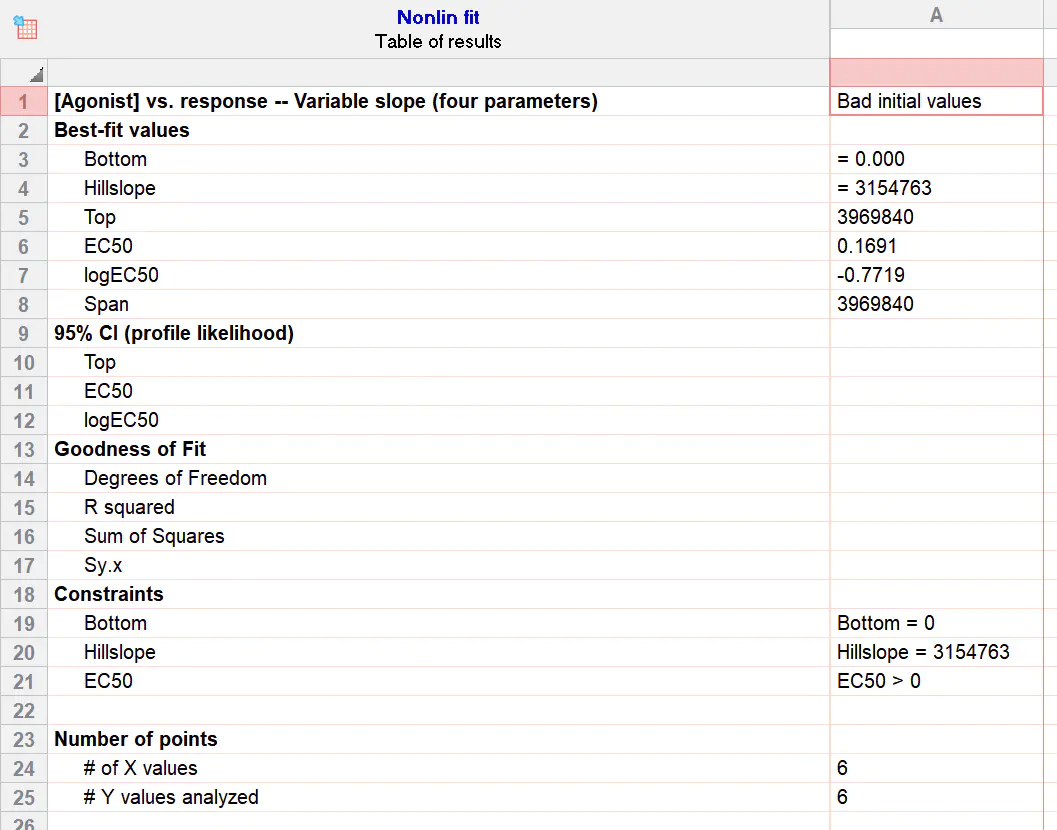
最后一个问题,NT50 应该用 Dose-response -Stimulation 还是 Dose-response -Inhibition?判断标准很简单:如果随 x 数值增加,y 数值减少,用 Inhibition,否则用 Stimulation
数值稳定性问题
如下例,id1 遇 id2 数值很接近,id3 与 id4 很接近。然而,如果不限制 top 参数做拟合,在 Prism 得到的 50% titer 分别是 2112, ~8.993, 1406, ~1.387,明显不对
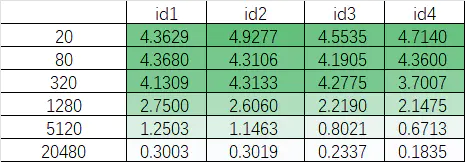
这可能是因为 id2、id4 在 80、20 两个 titer 间数值差别过大,导致 top 的拟合出现问题,从而影响到 50% titer
解决方法有两个,第一是指定 top 参数的值。第二是调整 titer,使用 -\lg \frac {1} {titer},这会让 titer 值更平滑
总结
以上,我们介绍了 NT50、IC50、EC50 的概念,并以 IC50 为例,使用 R 语言和 Prism 分别进行了计算。
由于实验条件、上下限设置的不同,同一个药物的 IC50 略有差异是正常现象,但一般少有数量级的变化。
如果你需要更深入的了解,可以去看 drc 包的原始参考文献:Dose-Response Analysis Using R | PLOS ONE
